Three-Point Estimating: Definition, Formula, and How to Use It

A large number of projects fail because teams often make inaccurate estimates for time, cost, and effort. Most methods end up relying on a single guess, ignoring risk and uncertainty. This problem can easily be solved by three-point estimating because it uses a range of values instead of just one. 

Project managers use three-point estimating method when they want more accurate forecasts. This estimation technique works well for time estimation, cost estimation, and effort estimation. It is often used in planning tools like the Program Evaluation Review Technique (PERT) and the Critical Path Method.

This guide explains how the method works and how it differs from single-point estimating. It covers the two main approaches it uses, triangular distribution and beta distribution (PERT), and shows how they relate to concepts like standard deviation. You’ll also learn how project teams use PERT charts to estimate timelines more accurately.

Three-point estimating gives you better control by showing what’s possible, what’s most likely, and what could go wrong-so your project stays on track.

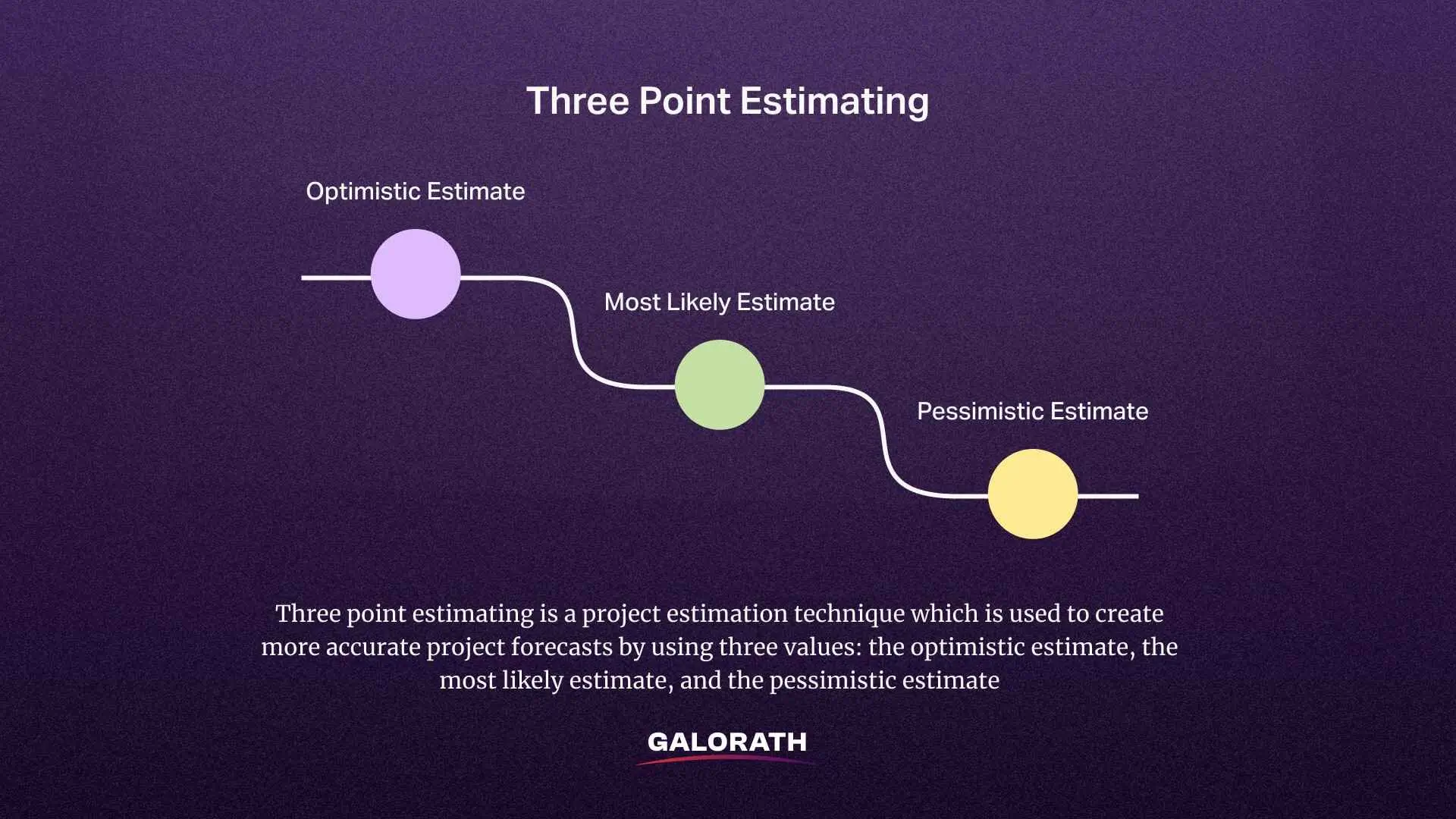
What is Three-Point Estimating?

Three-point estimating is a project estimation technique used to create more accurate project forecasts by utilizing three values: the optimistic estimate, the most likely estimate, and the pessimistic estimate. Instead of guessing a single number, teams calculate an expected duration or cost that reflects uncertainty in the task or activity. This method improves estimation accuracy because it shows a range of potential outcomes. 

Project managers often use it in project management when they plan for activity duration, time estimation, or cost estimation. It gives them a better chance to spot risks and plan resources wisely. This estimation method enhances both accuracy and objectivity in activity time estimation, especially when handling uncertainty.

Where is Three-Point Estimating Used?

Three-point estimating is one of the core estimation techniques used in project management to improve the accuracy of project forecasts. Teams use it when they want to reduce uncertainty and plan for a range of possible outcomes instead of relying on a single guess.

Compared to single-point estimating, this method offers a more flexible and realistic approach, especially when data is incomplete or when risk is high. Three-point estimates reduce the subjectivity and uncertainty regarding the anticipated start time of the proposed activity, helping improve both accuracy and objectivity in project scheduling.

Project managers apply three-point estimating in key areas of planning, including:

• Effort estimation – to forecast how much work a task will require
• Cost estimation – to predict the budget range for an activity or project
• Time estimation – to determine how long tasks or milestones will take

This method is especially useful during the early phases of a project, where exact values are hard to define. Unlike fixed-value methods that ignore uncertainty, three-point estimating techniques help teams make informed decisions by factoring in the optimistic, most likely, and pessimistic scenarios. 

Project teams also use this method to support resource allocation, improve planning accuracy, and identify potential delays or risks in the project schedule. Incorporating three-point cost estimation into project planning models improves sustainability outcomes and enhances decision-making by accounting for variability.

How Three-Point Estimating Works?

Three-point estimating works by defining three input values for each task: an optimistic estimate, a most likely estimate, and a pessimistic estimate. Teams use these values to calculate the expected duration or cost of a task, rather than relying on a single estimate. This approach helps reduce uncertainty and improves estimation accuracy. 

Here’s how each estimate type is defined:

• Optimistic estimate (O): This is the best-case scenario. It is created by assuming everything goes as planned-no delays, no obstacles, and ideal resource availability.
• Most likely estimate (M): This is the most realistic outcome. It is based on past experience, current resources, and known risks. It reflects the typical duration or cost if things go normally.
• Pessimistic estimate (P): This is the worst-case scenario. It is calculated by assuming delays, complications, or low resource availability.
  

After defining these three values, teams use them in one of two statistical models to calculate an expected outcome. Triangular and beta distributions (PERT) are commonly used for task time estimations in project management, with the triangular distribution treating all estimates equally. In contrast, the beta distribution (PERT) puts more weight on the most likely estimate to better reflect the typical project scenario.

Both models assume a normal distribution of outcomes, where the most likely result is the central point. However, they tend to produce different results. PERT beta distribution usually smooths out extreme values better, making it more suitable for complex projects. 

The triangular distribution, on the other hand, is simpler and useful when teams have limited data. The choice between triangular and beta distributions can significantly affect the results of project estimations, with PERT often yielding more robust predictions in complex scenarios.”

What Is Triangular Distribution?

Triangular distribution is a simple statistical model used in three-point estimating to calculate an expected duration or cost when you have limited data. It assumes that the best estimate lies somewhere between an optimistic, most likely, and pessimistic value, with all three estimates treated equally. 

Triangular distributions are generally preferred as task time probability distributions, due to their simplicity and ease of use in the absence of detailed historical data.

Formula for Triangular Distribution

To calculate the expected value using this model, the following formula is applied:

Expected Value = (Optimistic + Most Likely + Pessimistic) / 3

This formula gives a basic average of the three inputs, without placing more weight on any specific estimate.

When to Use Triangular Distribution

Triangular distribution is used when:

• There isn’t enough historical data for a more complex model
• A quick, easy-to-understand estimate is needed
• All three estimates seem equally likely

Project managers often apply triangular distribution during early planning stages or in smaller projects where time and resource constraints prevent deeper statistical analysis. Although it’s not as accurate as the PERT beta distribution, it still improves estimation accuracy over single-point guessing and helps teams visualize a realistic outcome range. 

According to Aliyu Am, “Triangular distribution is often a useful tool when data is limited and a quick estimate is necessary.” Still, it may not be as effective for more complex projects that require more sophisticated models like PERT.

What Is Beta Distribution (PERT)?

Beta distribution (PERT) is a weighted statistical model used in three-point estimating to calculate the expected duration or cost of a project task. It improves estimation accuracy by placing more emphasis on the most likely estimate, making it more realistic than the triangular distribution when data is uncertain or variable. 

As Nickos Papadatos highlights, “The beta distribution (PERT) is effective in cases where task duration estimates are uncertain, as it allows for more weight to be placed on the most likely estimate”.

PERT Formula (Beta Distribution)

To calculate the expected value using PERT, use this formula:

Expected Value = (Optimistic + 4 × Most Likely + Pessimistic) / 6

This formula increases the weight of the most likely estimate, reducing the influence of extreme values (optimistic and pessimistic) and providing a more balanced forecast. According to Maciej Wolny, “The beta distribution (PERT) places significant emphasis on the most likely estimate, which helps provide more realistic forecasts for project durations”.

How PERT Differs from the Basic Beta Distribution?

While both PERT and the generic beta distribution use probability curves, PERT simplifies the beta model by assuming a fixed shape and using only three parameters: optimistic, most likely, and pessimistic. 

Traditional beta distribution, in contrast, requires shape parameters (α and β), making it more complex and flexible but harder to apply in practical project settings. As Budi Eko Prasetyo notes, “PERT simplifies the beta distribution by using three time estimates and is more commonly used in project management due to its practical applicability”.

PERT makes the beta model easier to use by:

• Standardizing the weight formula
• Removing the need for advanced statistical inputs
• Fitting naturally into project planning tools like PERT charts

The simplicity and adaptability of PERT make it a preferred method for project managers who need a quick and effective way to estimate task durations and costs, as explained by Nova Nevila Rodhi.

When to Use PERT (Beta Distribution)

Project managers use the PERT beta distribution most frequently in:

• Large or complex projects where uncertainty is high
• Early planning stages, when detailed data is limited
• Critical path method analysis
• Situations requiring schedule planning with greater confidence

Because of its ability to reduce the impact of extreme estimates, PERT helps teams create more reliable forecasts and improve overall planning accuracy.

What Is a Standard Deviation?

Standard deviation measures how much variation or uncertainty exists in a set of values. In three-point estimating, it shows how far the actual outcome may spread from the expected duration or cost. A smaller standard deviation means your estimate is more consistent and reliable. 

A larger one indicates higher risk or uncertainty. Standard deviation plays a crucial role in risk analysis and project management as it provides a clearer picture of potential fluctuations in project estimates.

Formula for Standard Deviation (PERT)

In the context of PERT beta distribution, the standard deviation is calculated using this formula:

Standard Deviation = (Pessimistic – Optimistic) / 6

This formula uses the pessimistic and optimistic estimates to measure the range of uncertainty. It assumes that most outcomes fall within this range and follow a normal distribution. The standard deviation calculated using PERT is vital in understanding the spread of potential outcomes and is crucial for effective project planning.

How Standard Deviation Affects Results?

Standard deviation plays a key role in risk analysis and planning accuracy:

• A low standard deviation suggests that your estimate is stable and close to the most likely outcome.
• A high standard deviation signals more uncertainty and a wider range of possible results.

Project managers use standard deviation to:

• Assess confidence levels in schedules and budgets
• Add buffers or contingency reserves
• Identify tasks with high uncertainty risk

Including standard deviation in your estimates helps teams manage expectations and prepare for potential delays or cost overruns. According to Parlindungan Manik, “Integrating standard deviation into project management estimations helps project teams quantify uncertainty, enhancing decision-making and risk management”.

Normal vs Triangular Distribution vs PERT

Three-point estimating can use different distribution models depending on the level of accuracy and risk tolerance. The three most common are the normal distribution, triangular distribution, and PERT beta distribution. Each model uses the same input values-optimistic, most likely, and pessimistic-but produces different results based on how it treats those values.

Let’s compare the results using the following input estimates for a task:

• Optimistic (O) = 40 days
• Most Likely (M) = 60 days
• Pessimistic (P) = 100 days
  

Estimation Model Comparison Table

Model	Formula	Result (in days)	Weight on Most Likely	Risk Handling
Triangular Distribution	(O + M + P) / 3	66	Equal weight	Basic estimate
PERT (Beta Distribution)	(O + 4M + P) / 6	63	Heavily weighted	Better smoothing
Normal Distribution	Based on historical mean + std. Dev.	60 (assumed)	Assumes symmetry	Statistical projection

Key Differences

• Triangular distribution offers a simple average but doesn’t reduce the impact of extreme values.
• PERT beta distribution improves estimation accuracy by emphasizing the most likely outcome and reducing risk from outliers.
• Normal distribution assumes symmetrical spread around the mean and works better when you have enough historical data and a known standard deviation.

Project managers choose the model based on how much data they have, how risky the task is, and how precise the estimate needs to be.

What Is a PERT Chart?

A PERT chart is a visual project management tool that maps out the sequence of tasks, their estimated durations, and their dependencies. It stands for Program Evaluation Review Technique, and it helps teams schedule, organize, and coordinate complex projects.

The PERT chart is a key tool for project managers to visualize the task dependencies and durations, which allows for better project planning and resource allocation.

Project managers use PERT charts to identify the critical path-the longest sequence of dependent tasks that determines the minimum time needed to complete a project. This allows them to plan efficiently, allocate resources, and detect possible delays before they happen. 

Identifying the critical path in a PERT chart is essential for project success as it helps project managers focus on the most crucial tasks to ensure timely project completion.

How to Create a PERT Chart?

To build a PERT chart, follow these steps:

1. List all project tasks – Break the project into smaller activities or milestones.
2. Define task dependencies – Identify which tasks must be completed before others can start.
3. Apply three-point estimating – For each task, define the optimistic, most likely, and pessimistic durations.
4. Calculate expected durations – Use the PERT beta distribution formula to compute the expected time for each task:
   
   • (O + 4M + P) / 6
     
5. Create a network diagram – Draw nodes for each task and connect them based on dependencies.
6. Identify the critical path – Highlight the longest path through the network. These tasks determine the overall project duration.

Three-Point Estimating vs. Single-Point Estimating

Single-point estimating uses just one value to estimate the duration, cost, or effort for a task. This value usually comes from expert judgment or historical data and assumes that the estimate will occur exactly as predicted-without variation.

While this method is simple and fast, it doesn’t account for uncertainty, making it less reliable in complex or high-risk projects.

Teams then calculate an expected duration using either a triangular distribution or a PERT beta distribution, which helps reduce estimation errors by factoring in risk and variability.

Single point vs three-point Comparison Table

Feature	Single Point Estimating	Three-Point Estimating
Input	One value	Three values: O, M, P
Risk Handling	Ignores uncertainty	Accounts for uncertainty and variation
Accuracy	Lower	Higher due to weighted average
Use Case	Simple, low-risk tasks	Complex or high-risk tasks
Distribution Model	None	Triangular or PERT beta distribution
Planning Accuracy	Limited	Improved
Effort/Cost/Time Estimation	Basic	More realistic

Benefits of 3-Point Estimating

Three-point estimating offers several advantages over traditional estimation methods by improving accuracy, reducing risk, and enhancing decision-making. By incorporating optimistic, most likely, and pessimistic estimates, this method gives project managers a more complete picture of what could happen-rather than relying on a single assumption.

Improves Estimation Accuracy

Using a range of estimates instead of one fixed value helps teams produce more accurate project forecasts. The triangular distribution and PERT beta distribution provide structured ways to calculate the expected duration, factoring in possible delays or accelerations. This improves cost, time, and effort estimation for projects. By doing so, teams can set more realistic expectations with stakeholders.

Reduces Uncertainty and Risk

Three-point estimating accounts for uncertainty risk by modeling best-case and worst-case scenarios. This approach helps identify potential delays early in the planning process and prepares teams to adjust more effectively when problems arise.

It also supports:

• Better schedule planning
• More confident resource allocation
• Easier integration into tools like PERT charts and the Critical Path Method

Common Challenges of 3-Point Estimating

While three-point estimating offers greater accuracy and flexibility, it also comes with challenges that project teams must manage. These challenges can affect the quality of the estimates and the efficiency of the planning process if not addressed properly.

Difficulties in Gathering Reliable Input Data

One of the biggest challenges is collecting accurate optimistic, most likely, and pessimistic estimates. Team members may struggle to provide realistic inputs due to:

• Lack of historical data
• Limited experience with similar tasks
• Cognitive bias (too optimistic or too cautious)

Unreliable inputs can distort the expected duration and weaken estimation accuracy.

Time-Consuming Process for Complex Projects

Compared to single-point estimating, three-point estimating requires more time and effort. Teams must:

• Define three values for every activity
• Select a distribution model (either triangular or PERT beta distribution)
• Perform additional calculations

For large or fast-moving projects, this added complexity may delay planning or increase the risk of inconsistencies.

How to Use Three-Point Estimating in Practice

Organizations and project teams use three-point estimating to improve planning, control risk, and make better decisions across various areas of project management. This method is widely applied in industries like engineering, construction, IT, and product development, especially where time, cost, and scope are difficult to predict with certainty.

How Teams Use It in Real Projects

In practice, teams use three-point estimating techniques during early project planning or during risk assessment phases. They often follow this process:

1. Define the task – Break work into manageable units
2. Estimate three values – Gather input for optimistic, most likely, and pessimistic durations or costs
3. Select a distribution model – Use either the triangular distribution or the PERT beta distribution
4. Calculate expected values – Apply the formulas to derive the expected duration or cost
5. Integrate into planning tools – Feed estimates into scheduling tools and risk models

This process helps companies improve planning estimation accuracy, support resource allocation, and identify potential delays before they impact the project.

Example of Three-Point Estimation in a Real Project (Software Development)

Let’s look at how a software development team used three-point estimating to plan a key feature in a mobile app project. The task: developing a user authentication module that includes login, registration, password recovery, and integration with social login APIs.

Step 1: Break Down the Task

The team broke the module into smaller tasks:

• Backend API development
• Frontend UI integration
• OAuth setup for social logins
• Testing and bug fixing

Step 2: Apply Three Estimates for a Task

For the “OAuth setup” task, the team used historical data and developer experience to estimate:

• Optimistic estimate (O) = 2 days (if all APIs work as expected)
• Most likely estimate (M) = 4 days (based on similar past tasks)
• Pessimistic estimate (P) = 7 days (if third-party APIs have issues or delays)

Step 3: Choose a Distribution Model

Since this task involved moderate complexity and external dependencies, the team used the PERT beta distribution formula to calculate the expected duration:

Expected duration = (O + 4M + P) / 6
= (2 + 4×4 + 7) / 6
= (2 + 16 + 7) / 6 = 25 / 6 = 4.17 days

Step 4: Integrate Into Project Plan

The team used this estimate in their sprint planning and flagged the task for potential delays. They also used standard deviation = (P–O) / 6 = (7 – 2) / 6 = 0.83 days to assess the task’s risk.

Impact of Using Three-Point Estimating

• Team avoided over-committing on deadlines
• Schedule planning and resource allocation were improved
• Risks were communicated clearly to stakeholders
• Team used the estimate to update the PERT chart and monitor activity duration.

How Is Three-Point Estimating Connected to Risk Management?

Three-point estimating directly supports risk management by modeling uncertainty and accounting for possible variations in project outcomes. Instead of assuming a single fixed value, this method uses optimistic, most likely, and pessimistic estimates to reflect a full range of potential scenarios for each task or activity. 

By incorporating multiple estimates, three-point estimating enables project managers to more effectively handle uncertainty and account for the potential risks that might arise during project execution.

This method is particularly valuable in high-risk projects where the uncertainty of outcomes can significantly impact timelines and costs. 

In three-point estimating, the use of optimistic, most likely, and pessimistic values allows project managers to anticipate a range of potential results, thereby improving the overall accuracy and reliability of project forecasts.

Why It Matters for Risk Management

Quantifies Uncertainty

By incorporating the best- and worst-case scenarios, three-point estimating helps teams identify potential delays, cost overruns, or effort spikes early in the planning phase. This makes risks measurable rather than subjective.

Supports Contingency Planning

The method provides a calculated standard deviation for each estimate, which helps teams determine how much buffer or reserve time and cost to add. This supports smarter resource allocation and more accurate risk responses.

Improves Forecast Reliability

When used with models like the PERT beta distribution, three-point estimating improves estimation accuracy by reducing the influence of extreme values while still considering them. This leads to more realistic timelines and budgets.

Feeds into Broader Risk Analysis

Project managers use outputs from three-point estimates in:

• PERT charts for identifying risky paths
• Critical path method to find tasks that can delay the entire project
• Monte Carlo simulations (in advanced risk modeling)