Parametric Estimating for Accurate Project Predictions

Parametric estimating, a powerful algorithmic estimation methodology, enables organizations to predict project outcomes with remarkable precision. This methodology identifies statistical relationships between measurable project characteristics and historical results. Parameter-driven forecasting establishes reliable cost forecasting models during critical early planning stages, where funding and scope decisions have a significant impact. 

Unlike conventional methods relying on subjective judgment or exhaustive breakdowns, predictive cost modeling harnesses comprehensive historical performance data, supported by advanced statistical estimation methods, to deliver defensible forecasts with quantifiable confidence levels.

Parametric estimating relies on mathematical relationships and normalized historical data to produce consistent, scalable predictions. This approach forms the foundation for advanced cost and schedule models used across complex project environments. Its real-world impact can be seen in sectors like software development, manufacturing, aerospace, and defense, where accuracy and repeatability are critical to planning and execution.

Sophisticated methods for quantifying uncertainty and risk, such as probabilistic analysis, play a vital role in improving predictive cost modeling. These techniques offer actionable insights for organizations aiming to strengthen estimation accuracy and make better-informed planning decisions.

Parametric estimating provides a crucial solution to persistent project estimation challenges, particularly during conceptual phases where technical definitions are limited. Its rigorous, data-driven framework offers the confidence needed to navigate complexity. Parametric estimating is a vital tool for executives, project managers, and estimators seeking to achieve optimal project outcomes. 

This methodology enables rapid scenario analysis and produces well-documented, defensible estimates. It supports regulatory compliance and helps prevent project overruns, promoting accountability and project success.

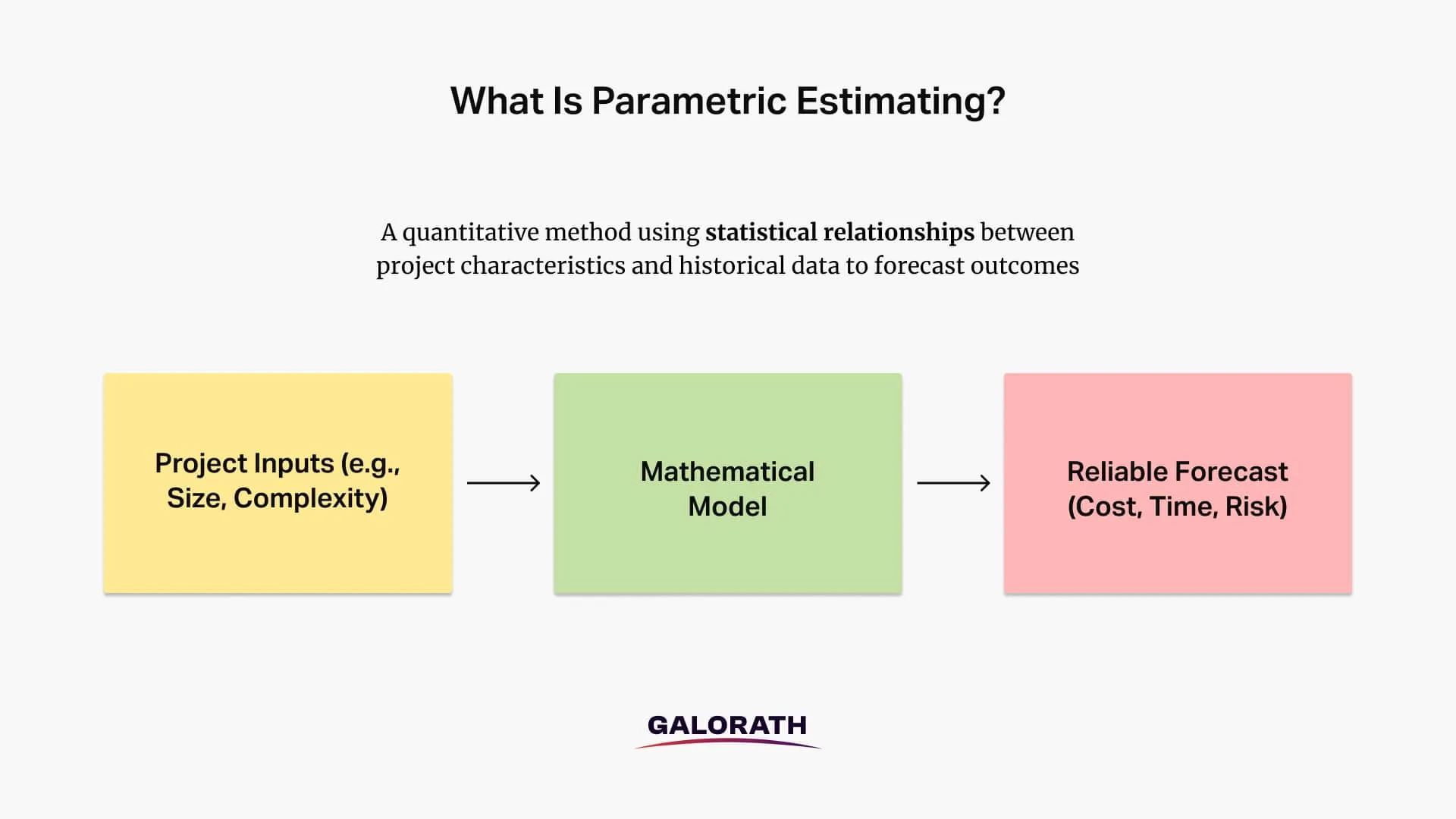
What Is Parametric Estimating?

Parametric estimating is a quantitative forecasting method that defines mathematical relationships between project characteristics and outcomes. In project management, this methodology translates to developing highly reliable forecasts for project costs, schedules, resources, risk, and effort allocation. This methodology leverages statistical correlations in historical data to predict outcomes for new projects, providing an alternative to methods that rely on subjective judgment or exhaustive breakdowns.

The Project Management Institute (PMI) further defines parametric estimating as a project estimation technique that uses a statistical relationship between historical data and other variables to calculate a project cost and time (or resources), as outlined in the Project Management Body of Knowledge (PMBOK).

Think of it like a seasoned chef who knows exactly how much salt is needed for a dish based on the amount of flour, even without tasting it: they’ve learned the statistical correlation over years of experience. This statistical correlation is the essence of parametric estimation, allowing for reliable predictions even with limited information.

As the U.S. Government Accountability Office (GAO) defines it in their “Cost Estimating and Assessment Guide” (GAO-20-195G, Page 169), “A parametric cost estimating technique uses a statistical relationship between historical costs and other program variables such as system physical or performance characteristics, contractor output measures, or manpower loading.”

The methodology’s effectiveness stems from its ability to establish reliable predictions even with evolving project details. Its name originates from “parameters,” which are measurable attributes (e.g., size, complexity, technology type) that act as independent variables in estimation formulas. 

As a core principle, estimating by parametrics is a method to show how these parameters influence cost, allowing estimators to develop Cost Estimation Relationships (CERs) that precisely predict future results based on the historical correlation of these parameters with project outcomes. Each resulting parametric estimate provides a defendable and statistically sound projection.

Parametric estimating’s strength lies in its inherent repeatability and traceability. This methodology formalizes cost logic with rigorous statistical analysis, replacing subjective guesswork with defensible, early-phase forecasting. Its structured approach facilitates the rapid generation of credible estimates for vital processes such as trade studies, budget reviews, and cost realism assessments, particularly when project scope remains fluid.

When Is Parametric Estimating Used?

Parametric estimating is used in four key situations: early project phases, supporting strategic decisions, quantifying risk, and meeting regulatory or compliance requirements. Its data-driven approach adapts well to changing information and diverse decision-making needs throughout the project lifecycle. This methodology, utilizing statistical models derived from historical performance, enables organizations to make informed decisions to restructure scope, increase budgets, or reconsider approaches before committing substantial resources.

1. During Early Project Phases

Parametric estimating proves invaluable during early project phases, delivering reliable forecasts when information is limited. The U.S. Government Accountability Office (GAO-20-195G) confirms its value in conceptual or preliminary design stages, where detailed specifications are still under development. This method enables critical, informed decision-making before committing substantial resources to a project direction.

This early warning system prevents major project overruns by identifying a low probability of success with current parameters. It enables organizations to proactively restructure their scope, increase budgets, or reconsider approaches, thereby mitigating unrealistic expectations and avoiding painful adjustments later.

2. For Strategic Decision Support

Parametric estimating proves indispensable for evaluating multiple alternatives swiftly, excelling at rapid “what-if” analysis. This capability enables comprehensive comparisons of diverse approaches, technologies, or designs, providing valuable insight during project feasibility assessment. For infrastructure megaprojects like high-speed rail initiatives, this approach often reveals significant disconnects between initial estimates and likely outcomes when comparing proposed budgets against statistical models.

3. When Quantifying Risk and Uncertainty

Parametric estimation is critical for projects where effective risk management is paramount. This methodology goes beyond qualitative assessments to precisely quantify estimation risk. Combined with Monte Carlo simulation, parametric estimation delivers quantified confidence levels for project outcomes, moving beyond misleading single-point estimates. This powerful capability empowers decision-makers to understand both the expected cost and the probability of achieving various cost targets, enabling risk-based contingency planning and more informed budget decisions.

4. For Regulatory and Compliance Requirements

Choose parametric methods when projects must satisfy stringent regulatory requirements for estimation rigor. Government contracts and regulated industries frequently demand statistically defensible estimates, substantiated by clear audit trails. Parametric estimation consistently fulfills these demands through its mathematical foundation and meticulously documented methodology.

Why Use Parametric Estimating?

Parametric estimation is mostly used because it improves early-stage accuracy, provides unbiased data-driven objectivity, enables risk quantification, accelerates scenario analysis, supports continuous model improvement, and delivers strategic value for competitive bidding and project planning. These advantages makes it to be one of the most preferred project estimating techniques for organizations seeking reliable estimates and better decision-making throughout the project lifecycle. 

1. Improves Early-Stage Accuracy

Parametric estimation consistently delivers substantial improvements in forecast reliability, particularly during early project phases. A study by the International Cost Estimating and Analysis Association found that companies utilizing calibrated parametric models significantly reduced average estimation error from 30-45% to a range of 10-20% for conceptual phase estimates. This translates directly to enhanced business outcomes, including more reliable capital planning, competitive bidding, and fewer mid-project financial surprises.

2. Provides Unbiased, Data-Driven Objectivity

Parametric estimation inherently eliminates cognitive bias by anchoring forecasts in verifiable statistical relationships rather than individual judgment. Research in behavioral economics consistently demonstrates human estimators are prone to optimism bias, anchoring, and the planning fallacy. Parametric methods directly counteract these psychological tendencies through their mathematical foundation, ensuring a superior degree of objectivity.

This data-driven objectivity provides a defensibility that subjective methods cannot match. It empowers estimators to precisely demonstrate their conclusions with supporting statistical relationships, historical data, and confidence levels, fostering trust and transparency.

3. Helps with Risk Quantification & Management

Parametric methods explicitly model cost uncertainty and risk exposure, precisely quantifying estimation risk. Through techniques like probabilistic modeling, parametric estimation generates ranges of possible outcomes with associated probabilities, enabling precise risk management. This leads to more sophisticated planning, appropriate contingency reserves, and decisions made with full awareness of inherent uncertainties.

4. Accelerates Scenario Analysis & Strategic Planning

Parametric models offer unparalleled speed in evaluating alternatives, particularly once the initial framework is established. By adjusting input parameters, teams swiftly assess multiple design approaches, technology options, or resource configurations without rebuilding estimates from scratch. This capability streamlines the decision-making process, allowing for comprehensive cost-benefit trade studies and rapid exploration of alternatives.

This speed facilitates the exploration of far more alternatives than traditional methods, leading to optimized solutions and more informed choices. This includes the evaluation of schedule compression scenarios, analysis of resource allocation strategies for multiple simultaneous projects, and quantification of cost impacts related to technical requirements or specification changes.

5. Continuously Improves System Performance

Each completed project actively enriches the parametric estimation knowledge base, creating a virtuous cycle of increasing accuracy over time. New historical data are systematically collected and incorporated, refining existing estimation models. This self-improving nature, driven by model calibration and refinement of statistical relationships, ensures forecasts remain current and relevant, reflecting the latest organizational performance.

6. Supports Competitive Bidding and Project Planning

Parametric estimating delivers significant strategic value by enhancing competitive bidding and project planning. Its ability to generate quick, defensible, and reliable estimates allows organizations to submit more accurate and competitive bids, improving their chances of securing projects. Furthermore, by providing early insights into potential costs, schedules, and risks, it enables proactive and more effective project planning, ensuring resources are allocated optimally and expectations are set realistically from the outset. This systematic methodology transforms estimation into a core strategic capability, supporting informed decision-making throughout the entire project lifecycle.

How Parametric Estimating Supports Cost, Schedule, Risk, and Effort Management?

Parametric estimating provides a framework that significantly enhances management across the critical dimensions of cost, schedule, risk, and effort, particularly in complex project environments.

Improves Cost Estimation Accuracy

Parametric cost estimating is a specialized application of parametric principle which precisely models relationships between project parameters and various cost categories. This methodology allows for accurate forecasts of total project cost, development cost, and production cost. While the overall project cost is the dependent variable, understanding the cost per unit value for specific parameters can enhance accuracy. By leveraging historical data through regression and statistical analysis, parametric cost estimating helps create accurate project budgets.

Enhances Timeline Planning

Parametric estimating fundamentally transforms timeline planning by providing reliable foresight into project durations. This approach enables teams to estimate activity duration using parametric models for entire projects or specific phases. Parametric estimating clarifies the overall project timeline by breaking down complex activities into quantifiable parameters, facilitating the creation of realistic schedule duration estimates. Ultimately, this precision in forecasting directly impacts delivery timeframes, ensuring projects meet their deadlines and strategic objectives.

Quantifies Estimation Risk

Parametric estimating significantly improves risk management by moving beyond qualitative assessments to quantify estimation risk. Through statistical techniques and probabilistic modeling, parametric estimating analyzes potential variations in project outcomes. This capability allows organizations to understand cost uncertainty and risk exposure with greater clarity, expressed through precise confidence intervals. By integrating probabilistic modeling, decision-makers gain a comprehensive view of possible scenarios, enabling proactive risk mitigation strategies and improved contingency planning.

Forecasts Labor Demand

Parametric estimating provides powerful tools to accurately forecast labor demand, crucial for efficient project execution. This methodology enables precise projections of staff-hours required for various project activities, leading to more realistic labor estimates. Parametric estimating helps organizations manage their human resource demand effectively, preventing both overstaffing and critical shortages. By applying parametric models, project managers generate reliable effort projections, ensuring the right personnel are available at the right time, optimizing productivity and minimizing operational costs.

What Are the Two Types of Parametric Estimates?

Parametric estimating fundamentally produces two distinct types of results, each serving different project needs by addressing uncertainty in varying ways.

1. Deterministic Estimates

Deterministic parametric estimates provide a single, specific value for cost, schedule, or resource requirements. This approach generates a particular number rather than a range, simplifying communication and facilitating straightforward planning. 

Deterministic estimates are often employed for preliminary planning or budgeting in projects with well-defined parameters or low complexity, where a quick, initial estimate is prioritized over detailed precision. A key limitation of deterministic estimates is that they inherently do not account for uncertainty or risk present in project inputs or models, providing a single-point precision that may be misleading in complex or high-risk environments.

For example, a deterministic model might state that a software module will require exactly 245 person-hours to develop, based on its function point count and complexity rating.

2. Probabilistic Estimates

Probabilistic parametric estimates explicitly acknowledge and quantify project uncertainty. Unlike deterministic methods, they provide a range of possible outcomes, each with an associated probability. 

This approach leverages sophisticated statistical techniques, such as Monte Carlo simulation, to generate thousands of scenarios and distributions of potential results. This capability provides a more comprehensive view of potential risks and opportunities, allowing project teams to understand the likelihood of different cost or schedule outcomes and set realistic confidence levels for estimates (e.g., P10, P50, P90).

As Dr. David Hulett, a pioneer in project risk analysis, advocates in Integrated Cost-Schedule Risk Analysis, understanding a range of possible outcomes is crucial, moving beyond reliance on single-point estimates.

Probabilistic estimating represents a significant evolution in forecasting practice, moving beyond false precision towards genuine accuracy. It is ideally suited for complex, high-risk projects where uncertainty is substantial, empowering stakeholders with a deeper understanding of potential risks and opportunities for more sophisticated planning and risk management. By embracing uncertainty, this method helps decision-makers make informed choices with full awareness of what is known and what remains uncertain.

Three-Point Estimates in Probabilistic Parametric Estimation 

The point-estimation is a core component of probabilistic parametric estimation, explicitly capturing project uncertainty and variability. This forecasting technique requires project teams to define an optimistic estimate (best-case scenario), a most likely estimate, and a pessimistic estimate (worst-case scenario) for each key variable. These three values form the basis for probability distributions used in advanced techniques such as Monte Carlo simulation. 

Probabilistic parametric estimation generates a more realistic forecast of potential outcomes, by using a range of possible values instead of a single point. This method quantifies the likelihood of different results, allowing teams to set confidence levels (such as P10, P50, P90( and make informed decisions about risk and contingency planning. 

For example, in cost estimation the optimistic value is the lowest plausible cost, the pessimistic value is the highest and the most likely value reflects the expected outcome. Monte Carlo simulation uses these three inputs to generate thousands of possible results, quantifying risk and showing the probability of different cost scenarios. 

As Dr. David Hulett argues in Integrated Cost- Schedule Risk Analysis, incorporating three-point estimates improves project planning by capturing uncertainty and providing a more realistic range of possible outcomes, which is crucial for reliable forecasting in complex and high-risk environments. 

Parametric vs. other Project Estimation Techniques

Estimation Technique	Input Requirements	Strengths	Limitations
Parametric	Measurable drivers + historical calibration	Fast, scalable, transparent, ideal for early-phase use	Requires validated data and calibrated models
Analogous	Historical data from similar projects	Fast, low cost	Subjective, limited traceability
Bottom-Up	Detailed Work Breakdown Structure (WBS)	Highly accurate with complete scope	Time-intensive, unusable in early stages
Expert Judgment	Professional intuition and experience	Flexible, suitable for novel or ambiguous projects	Prone to bias, lacks auditability

Parametric vs. Analogous (Comparative) Estimating

Understanding parametric estimating’s unique strengths requires a direct comparison with alternative approaches. Analogous estimating, also known as comparative estimating, uses similar past projects as comparison points, adjusting for differences through scaling factors. While superficially similar to parametric approaches, fundamental distinctions exist in their methodology and reliability.

Parametric estimating fundamentally relies on statistical relationships derived from multiple historical projects. It rigorously quantifies the mathematical relationship between project parameters and expected outcomes, providing statistical confidence levels for its forecasts. 

This methodology scales systematically across different project sizes, allowing for precise adjustments based on quantifiable data. To achieve this, a historical database and comprehensive statistical analysis are required.

In contrast, analogous estimating typically relies on one or a few reference projects. This method often involves subjective adjustments based on perceived differences between the current and past projects, which can introduce bias. Consequently, it offers limited confidence quantification, as its projections lack the statistical rigor of parametric models. Analogous estimating struggles with projects significantly different from historical references, making it less adaptable to novel technologies or unique complexities. Furthermore, it needs only limited reference project documentation, as its core premise is high-level similarity rather than detailed data analysis.

The practical difference between these two approaches becomes particularly evident when dealing with new technologies or components. Analogous methods often struggle in these scenarios because they rely heavily on overall similarity to past projects, which may not exist for truly innovative elements. 

For instance, a satellite development program incorporating a new propulsion system might share 80% identical components with a previous satellite. However, the novel technology creates unique estimation challenges that analogous methods cannot easily address due to their reliance on direct similarity.

Parametric estimation excels in such scenarios by modeling the specific impact of changing individual variables. It maintains valid estimates for common elements while providing more precise adjustments for variations than simple scaling from a single reference project. This rigorous mathematical approach allows for high accuracy and adaptability, especially when past experience is not directly comparable.

Parametric vs. Bottom-Up Estimating

Bottom-up estimating builds detailed estimates from component parts, summing individual work packages to create project totals. This approach stands in contrast to parametric estimation’s top-down methodology, offering distinct advantages and limitations depending on the project phase and available information.

Parametric estimating is a top-down approach that uses project characteristics to derive estimates. It works effectively with limited information during early project phases, making it suitable for conceptual planning. 

In contrast, bottom-up estimating is a bottom-up approach that relies on detailed components. It requires detailed specifications and designs, making it more suitable for later project phases. This method is time-intensive to create and revise due to the granular level of detail. Bottom-up estimates are superior for execution-phase planning and control because they provide a precise understanding of individual work packages. However, they can be slow and require significant effort upfront.

The most effective project management strategies often combine these methods. The Project Management Institute’s Practice Standard for Project Estimating recommends using multiple estimation methods as cross-validation. 

When parametric and bottom-up estimates align within an acceptable range, this convergence significantly increases confidence in the forecast. Experienced organizations leverage this complementary relationship: parametric models provide rapid, top-down validation for detailed estimates, while bottom-up methods offer granular insights that help refine parametric relationships. 

Parametric Estimation vs. Expert Judgment

Expert judgment relies on experience and intuition to create estimates without formal mathematical models. This traditional approach stands in stark contrast to the data-driven rigor of parametric estimation, each possessing unique strengths and limitations.

Dr. Harold Kerzner, in his influential work on project management, affirms that ‘the most accurate estimates emerge from approaches that combine statistical models with structured expert assessment.

Conversely, expert judgment is primarily based on individual experience and intuition. This reliance on subjective assessment means results can vary significantly between experts, leading to potential inconsistencies. 

Expert judgment often lacks transparent reasoning, as its basis is often tacit knowledge rather than documented calculations. However, it possesses the unique ability to address novel situations without precedent, where historical data may be unavailable. Its implementation depends on domain expertise, requiring seasoned professionals with deep knowledge of the specific project area.

The primary limitation of relying solely on expert judgment is its susceptibility to cognitive biases, including optimism bias and anchoring. Parametric methods actively counterbalance these tendencies through their data-driven objectivity. 

The most effective organizations integrate both approaches: they use parametric models for baseline estimates and then apply expert judgment to identify unique project circumstances that may necessitate adjustments.

Formula for Parametric Estimating

A formula for parametric estimating is a mathematical expression that quantifies the relationship between project characteristics (parameters) outcomes to determine project cost and duration effectively. These formulas are derived from statistical analysis of historical data, allowing for predictive modeling.

The general form of a parametric estimating formula can be expressed as:

Outcome = A × (Parameter)^B + C

Where:

• Outcome: The dependent variable being estimated (e.g., cost, schedule duration, effort).
• Parameter: The independent variable or measurable attribute of the project (e.g., lines of code, weight, square footage, complexity factors).
• A, B, C: Statistically derived coefficients (constant, exponent, and intercept, respectively) that quantify the historical relationship between the parameter and the outcome. These coefficients are determined through regression analysis of past project data.

For example, a software project might use code size (measured in thousands of lines of code (KLOC)) as a parameter to predict development effort through a Cost Estimation Relationship (CER):

Development Effort = 2.4 × (Code Size in KLOC)^1.05

This formula expresses a statistical relationship validated through historical project analysis. It indicates that every thousand lines of code typically requires 2.4 person-months of effort, with a slight scaling factor (1.05) to account for increasing complexity in larger projects.

Core Components of Parametric Estimation Models

Parametric estimation models, often referred to as mathematical models or algorithmic models, are structured frameworks that quantify relationships between project characteristics and outcomes. These models provide a systematic way to forecasting, acting as the computational engine for generating estimates based on established principles. Understanding their core components is essential to grasp how parametric estimation effectively works to produce reliable and defensible predictions.

1. Historical Data

Historical data forms the bedrock of all parametric estimation, with its quality, relevance, and analytical rigor directly determining the accuracy of forecasts. This approach operates on a fundamental principle: even sophisticated mathematical models cannot overcome poor historical data, underscoring the “garbage in, garbage out” maxim.

Parametric models rely on the systematic collection and analysis of past project information to identify patterns and relationships. Without accurate historical cost data and other quantifiable parameters from prior efforts, parametric estimation would lack its empirical foundation.

The Department of Defense further underscores this fundamental principle, stating that ‘the accuracy of any parametric estimate is directly related to the quality of the data used in its development.’ For data to be effectively utilized, it must be homogeneous – meaning consistent in its collection methods, definitions, and scope across different projects. This ensures that comparisons are valid and that statistical relationships accurately reflect underlying trends. 

The principle that “the more data, the better” generally holds true, as a larger volume of high-quality baseline project data enhances the statistical validity and predictive power of the models. This empirical evidence, derived from carefully analyzed past performance, allows estimators to identify the parameters that reliably influence project outcomes. The quality and availability of this historical data directly determine the accuracy and reliability of the resulting parametric estimates.

What is a Reliable Historical Database made out of?

Organizations looking to build out parametric capabilities must systematically collect comprehensive project data. A reliable historical database includes:

• Project characteristics: Size metrics, complexity factors, technology types, and other measurable attributes influencing outcomes.
• Final actual costs: Comprehensive cost data, consistently categorized across projects to identify spending patterns.
• Resource utilization: Labor hours, material quantities, and equipment usage, meticulously tracked against initial plans.
• Schedule performance: Variances between planned and actual durations for key activities and phases.
• Contextual factors: Environmental conditions, team experience, and organizational characteristics that might explain performance variations.

Normalization of the Data and making History Comparable

Raw historical data often contains inherent variations requiring normalization before modeling. The data normalization process transforms raw data into a standardized dataset, enabling actual patterns and relationships to emerge through rigorous statistical analysis.

Effective historical data normalization practices include:

• Inflation adjustment: Converting all cost data to a common base year using appropriate indices for different cost categories.
• Geographic normalization: Accounting for regional differences in labor rates, material costs, and productivity factors.
• Technology evolution: Adjusting for technological changes that affect productivity or capabilities over time.
• Learning curve effects: Recognizing production efficiency improvements occurring as quantities increase.
• Project-specific factors: Identifying and adjusting for unique circumstances that might distort comparative analysis.

2. Variables in Parametric Estimation: The Cost Drivers

Parametric estimation models are built upon the analysis of relationships between different types of variables, often referred to as “cost drivers”. These variables can be categorized based on whether they represent the outcome being predicted or the factors influencing that outcome.

Dependent Cost Variables

The dependent cost variable represents the outcome that the parametric model aims to predict. This is typically the total cost of a project, a specific phase, or a particular component. It is the variable whose value is dependent on changes in the independent variables (cost drivers). For example, in a software development project, the total person-hours required (which directly translates to development cost) would be a dependent cost variable.

Independent Cost Variables

Independent non-cost variables are the measurable attributes or characteristics of a project that influence the dependent cost variable. These are the “cost drivers” that the model uses to make predictions. They are “non-cost” because they do not directly represent a monetary value themselves, but rather physical, performance, or contextual characteristics. These parameters are identified and quantified based on historical data analysis, forming the basis for the statistical relationships within the parametric model. Examples include:

• Size metrics: Such as thousands of lines of code (KLOC) for software, square footage for construction, or weight for hardware.
• Complexity factors: Reflecting the intricacy of the design, interfaces, or functionality.
• Technology type: Indicating the maturity or novelty of the technology used.
• Performance characteristics: Like processing speed or throughput for a system.
• Contextual factors: Such as team experience, organizational efficiency, or regulatory environment.

3. Cost Estimating Relationships (CERs)

Cost Estimating Relationships (CERs) form the mathematical heart of parametric estimation, serving as fundamental building blocks within broader estimation models. These formulas mathematically express how independent variables, known as parameters, predict dependent variables (such as costs, schedules, and resources), all based on rigorous statistical analysis of historical data.

Estimation models transcend individual CERs by integrating them with crucial components like calibration, complexity modifiers, and scenario testing. This comprehensive framework allows for more nuanced and adaptable forecasting, leveraging the precision of CERs within a dynamic analytical environment. NASA, in its cost estimation guidance, underscores that effective CERs must demonstrate both statistical validity and a logical relationship to their estimation target, ensuring reliable forecasts.

Creating effective CERs follows a structured analytical process to ensure their predictive power and accuracy. This involves:

• Hypothesis development: Identifying potential relationships and assessing correlation between parameters and cost based on domain expertise.
• Statistical analysis: Employing regression techniques to perform a regression analysis and test proposed relationships and determine their correlation strength.
• Model selection: Evaluating alternative mathematical forms (e.g., linear, power, logarithmic) to identify the best fit for the analyzed data.
• Validation testing: Verifying the CER’s predictive power using reserved test data not utilized during model development.
• Statistical qualification: Ensuring the model meets stringent mathematical validity tests, incorporating metrics such as R² values and significance tests, alongside error analysis.

Single-Variable vs. Multi-Variable CERs

CERs adopt various mathematical forms depending on the underlying relationship patterns within the data. These forms broadly categorize into single-variable and multivariable structures.

Single-variable CERs express the outcome as a function of just one independent parameter. Examples include:

• Simple Linear: Cost = A + B × (Parameter) (e.g., software testing effort related to function points).
• Power Function: Cost = A × (Parameter)^B (e.g., aerospace weight-based CERs modeling the non-linear relationship between aircraft weight and development cost).

In contrast, multi-variable CERs incorporate two or more independent parameters to predict the outcome. These are essential for capturing the complexity of real-world projects where multiple factors influence results. Examples include:

• Multiple Regression: Cost = A + B × (Parameter1) + C × (Parameter2) (e.g., considering both part count and complexity factor).
• Complex Non-Linear: Cost = A × (Parameter1)^B × (Parameter2)^C (used for sophisticated relationships capturing interaction effects between parameters).

For instance, a manufacturing example illustrates the application of multi-variable CERs: analysis of production costs across multiple products reveals that assembly time correlates strongly with both part count and product complexity. Statistical regression can produce a hypothetical CER like:

Assembly Hours = A × (Part Count) + B × (Complexity Factor) + C

Here, A, B, and C are coefficients derived from statistical analysis of historical assembly data. This formula indicates that assembly time typically increases with both the number of parts and the complexity of the assembly process. Complex projects invariably require multiple parameters to predict outcomes adequately, making multi-variable CERs indispensable for comprehensive forecasting.

4. Regression Analysis & Calibration

Effective parametric estimation relies heavily on regression analysis and diligent model calibration. These processes ensure the statistical validity and practical applicability of the mathematical models used for forecasting project outcomes.

Regression Theory

Regression theory provides the statistical framework for modeling the relationships between variables in parametric estimation. This technique identifies and quantifies the strength and nature of connections between independent parameters (cost drivers) and dependent outcomes (costs, schedules, or effort). 

Through regression, estimators derive the coefficients for Cost Estimating Relationships (CERs), effectively translating raw historical data into predictive formulas. It allows for the systematic testing of hypotheses about how specific project characteristics influence results, forming the analytical backbone of algorithmic models.

Model Calibration

Model calibration is the iterative process of fine-tuning a parametric model’s parameters and coefficients to ensure its accuracy and relevance. This involves adjusting the mathematical models based on actual project results and refined historical data, thereby improving their predictive power. 

Effective calibration ensures that the model reflects the most current understanding of project drivers and performance. It is a critical step in the continuous improvement system of parametric estimation, ensuring models remain current, reliable, and closely aligned with the real-world performance of an organization’s baseline project data.

Curve Behavior

The mathematical models underlying CERs exhibit various curve behaviors when their relationships are plotted, reflecting different patterns in the data. Understanding these behaviors is crucial for accurate forecasting:

• Linear Curves: Represent a constant rate of change between parameters and outcomes, suggesting a straightforward, additive relationship.
• Power Functions: Often model non-linear relationships, where changes in parameters lead to increasingly or decreasingly proportional changes in outcomes, common in areas like technology evolution or learning curve effects.
• Logarithmic Curves: Can represent relationships where the rate of change decreases as the parameter increases, indicating diminishing returns.
• Complex Non-Linear Functions: Capture more intricate interactions between multiple parameters, essential for accurately representing highly complex systems.

Selecting the appropriate curve behavior ensures that the estimation models accurately reflect the true underlying relationships within the empirical evidence, enhancing the precision and reliability of the predictions.

5. Sensitivity Analysis

Sensitivity analysis is a crucial technique in parametric estimation that assesses how changes in specific input parameters or assumptions affect the estimated outcome. This analytical process systematically varies one or more cost drivers or other quantifiable parameters within a mathematical model to observe their individual impact on the final forecast.

The primary purpose of sensitivity analysis is to identify the most influential variables within an estimation model. By quantifying how much the predicted outcome changes in response to adjustments in different inputs, project teams gain critical insights into sources of cost uncertainty and risk exposure. This enables them to prioritize data collection efforts, refine assumptions, and focus risk management strategies on the variables with the highest potential impact on the project’s success.

Indeed, identifying the drivers of uncertainty in a model is a critical aspect of sensitivity analysis, revealing which inputs exert the most significant impact on the outputs.

Often performed in conjunction with Monte Carlo simulation, sensitivity analysis generates visual tools like tornado diagrams or scatter plots, clearly illustrating which parameters contribute most to the overall uncertainty in an estimate. This direct visualization supports risk-informed decision-making, allowing stakeholders to understand the critical drivers of project outcomes and allocate contingency funds more effectively. The following graphical image shows how parametric cost estimation works, step by step.

How to Implement Parametric Estimating Successfully?

Implementing parametric estimation successfully involves a structured, systematic process: building a parametric estimation model by establishing a historical database of project data and normalizing this information to ensure comparability across projects. . Rather than relying on guesswork, this methodology leverages historical data and statistical analysis through a series of key steps to produce accurate and defensible forecasts.

Here’s a unique list of the steps involved in performing parametric estimating:

1. Build a Structured Historical Database:
   • Description: Successful parametric estimation begins with systematic data collection. This involves developing a consistent project data architecture to capture crucial information from past projects.
   • Key Inclusions: Cost breakdowns following a standard structure, technical parameters and their evolution over time, schedule milestones and actual achievement dates, resource utilization patterns, and environmental and context factors.
   • Why It’s Important: A database provides the necessary empirical evidence for model development, ensuring the estimate is grounded in actual experiences from comparable programs.
     
2. Master Data Normalization Techniques:
   • Description: Raw project data often contains variations that must be addressed before modeling to ensure comparability. This involves systematically applying adjustments to past project data.
   • Key Adjustments: Inflation effects across different cost categories, geographic variations in labor and material costs, learning curve effects in production environments, technology evolution impacts on productivity, and organizational changes affecting performance.
   • Why It’s Important: Normalization transforms raw data into a standardized dataset, enabling actual patterns and statistical relationships to emerge, ensuring fair and proper comparisons for cost drivers.
     
3. Start with Simple Models and Evolve them:
   • Description: Rather than attempting comprehensive complexity immediately, begin with straightforward models focused on the strongest correlations in historical data. This recommends an iterative methodology to model development, starting with basic relationships and adding complexity only as needed to improve accuracy.
   • Why It’s Important: This strategy allows for validation of simple models before adding complexity, ensuring fundamental accuracy while scope and sophistication grow.
     
4. Combine with Expert Judgment:
   • Description: Strengthen parametric estimates by integrating expert judgment. This involves using experts to validate model outputs and applying experience-based adjustments for unique factors.
   • Why It’s Important: This hybrid approach helps reconcile differences between model results and expert opinion, and identifies when model assumptions might not apply, mitigating biases inherent in relying solely on data.
     
5. Create an Estimation Governance Framework:
   • Description: Establish formal processes for model development and maintenance. This framework instills discipline and prevents errors throughout the estimation lifecycle.
   • Key Elements: Model development and validation standards, required statistical qualifications, documentation requirements, version control and change management, peer review procedures, and continuous improvement mechanisms.
   • Why It’s Important: A well-defined governance structure ensures estimation quality and consistency across the organization.
     
6. Implement Formal Project Closeout Processes:
   • Description: Integrate data capture mechanisms into project closeout procedures. This ensures that new project data is systematically collected and incorporated into the historical database.
   • Why It’s Important: This step helps update existing models and ensures data quality through validation rules and governance procedures, fueling the continuous improvement cycle of parametric estimation.

Examples of Parametric Estimating

Here are two examples illustrating its application in IT and software development contexts:

Example 1: Estimating Software Development Effort

Scenario: A software development team needs to estimate the effort required for a new feature set within an existing application. Traditional detailed estimation would be time-consuming due to evolving requirements and unknown complexities.

• Parameter: Function Points (FP) – a common metric in software development that quantifies the functionality delivered to the user, independent of the programming language.
• Outcome: Development Effort (measured in person-months or person-hours).
• Historical Data: The organization has systematically collected data from dozens of past software projects, including their estimated function point counts and the actual development effort expended. Through statistical analysis, a Cost Estimation Relationship (CER) has been established.
• Application: A new feature set is analyzed and estimated to contain 150 Function Points. Applying the established CER (e.g., Development Effort (person-months) = 0.15 × Function Points + 5), the team can quickly predict the required effort: 0.15 * 150 + 5 = 27.5 person-months. This provides a rapid and defensible parametric estimate for resource planning and schedule forecasting.

Example 2: Forecasting IT System Migration Cost

Scenario: An IT department plans to migrate several legacy applications and their associated user bases to a new cloud-based infrastructure. They need a quick, high-level cost estimate before committing to a detailed migration plan.

• Parameter: Number of Active User Accounts (UACs) associated with each application.
• Outcome: Migration Cost (measured in USD).
• Historical Data: The IT department has historical data from previous system migrations, correlating the number of user accounts involved with the actual costs (including labor, software licenses, and infrastructure setup) for those migrations. This empirical evidence is analyzed using statistical methods to derive a reliable Cost Estimation Relationship (CER).
• Application: For a new application with an estimated 5,000 active user accounts, the IT department applies the CER (e.g., Migration Cost (USD) = 15 × UACs + 20,000). The predicted migration cost would be 15 * 5,000 + 20,000 = $95,000. This allows for swift budgeting and strategic decision support, enabling the organization to evaluate the financial implications of the migration without extensive upfront detailed planning.

7 Benefits of a Parametric Estimation Technique

Parametric estimation offers a range of significant advantages that drive its widespread adoption across industries, solidifying its role as a strategic capability for managing complex projects effectively. There are 7 benefits of using and doing parametric estimating:

1. Enhanced Early-Stage Accuracy & Predictability

This approach consistently delivers high forecast reliability, especially during initial project phases when information is scarce. Organizations report substantial improvements in forecast accuracy, allowing for more precise predictions of total project cost, development cost, and production cost. 

This capability enables proactive decision-making, ensuring resources are optimally allocated and expectations are set realistically from the outset.

2. Unbiased, Data-Driven Objectivity

Parametric estimation fundamentally eliminates cognitive bias by anchoring forecasts in verifiable statistical relationships rather than individual judgment. It actively counteracts psychological tendencies like optimism bias and the planning fallacy, ensuring a higher degree of objectivity in estimates. 

This data-driven objectivity provides a defensibility that subjective methods cannot match, allowing estimators to precisely demonstrate their conclusions with supporting historical data and confidence levels.

3. Risk Quantification & Management

Parametric methods explicitly model cost uncertainty and risk exposure, moving beyond qualitative assessments to quantify estimation risk. Through techniques like probabilistic modeling, it generates ranges of possible outcomes with associated probabilities, enabling precise risk management. This leads to more sophisticated planning, appropriate contingency reserves, and decisions made with full awareness of inherent uncertainties.

4. Accelerated Scenario Analysis & Strategic Planning

Parametric models are especially effective as an estimation model for complex projects and strategic decision support, offering unparalleled speed in evaluating alternatives. By rapidly adjusting input parameters, teams can swiftly assess various design approaches, technology options, or resource configurations without rebuilding estimates from scratch. 

This capability facilitates comprehensive cost-benefit trade studies, evaluates schedule compression scenarios, and optimizes resource allocation strategies for multiple simultaneous projects, transforming the decision-making process.

5. Continuous Improvement & Model Refinement

Each completed project actively enriches the parametric estimation knowledge base, creating a virtuous cycle of increasing accuracy. New historical data is systematically collected and incorporated, refining existing estimation models. This self-improving nature, driven by model calibration based on actual results and refinement of statistical relationships, ensures that forecasts remain current and relevant, fostering persistent organizational learning.

6. Improved Resource Optimization & Project Control

Parametric estimating directly contributes to efficient resource optimization and project control. It enables precise projections of staff-hours and labor estimates, ensuring the right human resource demand is met without over- or under-staffing. By generating reliable effort projections and detailed project timelines, it empowers teams to proactively manage schedules, optimize resource deployment, and maintain tight control over delivery timeframes throughout the project lifecycle.

7. Auditability & Stakeholder Confidence

Parametric estimation consistently delivers verifiable documentation that satisfies stringent audit requirements, making it ideal for regulatory and compliance-driven environments. Its outputs are derived from quantifiable statistical relationships and transparent mathematical models, providing defensible estimates that build strong stakeholder confidence. This clarity allows project teams to articulate their rationale precisely, ensuring trust in forecasts and reducing resistance from skeptical stakeholders.

8 Disadvantages and Limitations of Parametric Estimating

While parametric estimating offers significant advantages, it also comes with specific disadvantages and inherent limitations that project teams must acknowledge for effective implementation. These are the 8 most common disadvantages of parametric estimating:

1. High Dependency on Quality Historical Data

Parametric models are fundamentally reliant on the availability and quality of historical data. If this data is incomplete, inconsistent, or inaccurate, the resulting estimates will be flawed. The principle of “garbage in, garbage out” is acutely relevant here; even sophisticated mathematical models cannot overcome poor-quality empirical evidence. Organizations without a history of meticulously collected project data may find it challenging to implement parametric estimation effectively.

2. Risk of Misleading Accuracy Without Normalization

Raw historical data often contains variations—such as differences in inflation, labor rates, or technology levels—that must be carefully normalized. If data normalization techniques are not rigorously applied, the statistical relationships derived may be misleading. This can lead to a false sense of accuracy in the parametric estimate, as the model might identify correlations that are merely artifacts of unadjusted data rather than true underlying patterns.

3. Limited Applicability for Novel Projects

Parametric estimating’s reliance on past data makes it less suitable for truly novel projects or those with unprecedented technologies. If a project has no directly comparable baseline project data or quantifiable parameters from prior efforts, establishing reliable Cost Estimation Relationships (CERs) becomes difficult or impossible. In such scenarios, the approach offers limited value, as there’s insufficient empirical evidence to build predictive models.

4. Requires Specialized Expertise & Resources

Implementing and managing parametric estimation models effectively demands specialized skills. Organizations need professionals proficient in statistical analysis, regression theory, and model calibration. 

Developing and maintaining accurate mathematical models and algorithmic models also requires dedicated resources, including data collection systems and analytical tools, which may be a significant investment for some teams.

5. Potential for Over-Simplification of Complexity

While powerful, parametric estimation can sometimes over-simplify complex project realities. Focusing solely on a few cost drivers might overlook intricate interactions or nuanced factors that significantly influence project outcomes. This can lead to a model that, while statistically sound based on its chosen parameters, fails to capture the full scope of a project’s actual complexity, potentially resulting in an incomplete effort projection or schedule duration.

6. Challenges in Communicating Statistical Confidence

Explaining quantifiable uncertainty analysis and confidence intervals to non-technical stakeholders can be challenging. While probabilistic modeling provides a rigorous view of risk exposure, communicating these ranges and probabilities effectively requires careful translation. 

Over-reliance on numerical outputs without clear explanation can lead to misunderstanding or misinterpretation by stakeholders accustomed to single-point estimates, undermining the value of the sophisticated analysis.

7. Subjectivity in Parameter Selection & Adjustment

Despite its data-driven nature, parametric estimating retains elements of subjectivity, particularly in the initial selection of cost drivers and the subsequent adjustment of historical data. The choice of which parameters to include, how to normalize them, and even the selection of appropriate curve behavior for CERs can be influenced by expert judgment or organizational biases. This can affect the perceived objectivity and repeatability of the process if not transparently managed.

8. Risk of “Black Box” Perception

The advanced mathematical models and statistical methods underlying parametric estimation can sometimes be perceived as a “black box” by those without specialized knowledge. If the derivation and mechanics of the estimation models are not clearly communicated or understood, stakeholders may distrust the results. This lack of transparency can hinder adoption and limit the effectiveness of the approach, regardless of its inherent accuracy.

How to Make Parametric Estimating More Accurate?

Parametric Estimating can be made more accurate by using clean historical data, selecting the right cost drivers, integrating probabilistic modeling, and refining estimates with expert judgment. The precision of parametric estimation hinges significantly on the quality and relevance of historical data, but accuracy is a multifaceted goal requiring continuous effort across various dimensions of the estimation process. Here are the 4 ways to make parametric estimating more accurate:

1. Ensuring Historical Data Accuracy

The principle of “garbage in, garbage out” is paramount here. Historical data accuracy forms the absolute bedrock for reliable parametric models. To maximize accuracy, organizations must focus on:

• Rigorous Data Collection: Implement systematic and consistent processes for gathering baseline project data. This includes defining clear metrics, tracking methodologies, and ensuring data integrity from the outset.
• Comprehensive Data Normalization: Address variations in raw historical data through diligent normalization techniques. This involves adjusting for inflation, geographic differences in costs and labor, technology evolution, and learning curve effects to ensure quantifiable parameters are truly comparable. Without accurate normalization, statistical relationships derived from the data can be misleading.
• Data Validation: Regularly verify the quality, completeness, and reliability of collected data. Validate against actual project outcomes to identify and correct any discrepancies or errors that might distort the estimation models.

2. Refine Cost Driver Selection & Application

Accurate parametric estimation depends on the careful selection and application of cost drivers. To enhance precision:

• Identify Influential Parameters: Focus on cost drivers that demonstrate strong statistical correlation and logical causality with project outcomes. Prioritize parameters with high early availability and ease of measurement.
• Optimize CERs: Continuously refine Cost Estimation Relationships (CERs) through rigorous statistical analysis and model calibration. This involves evaluating different curve behaviors and mathematical forms to ensure the best fit for the data.
• Account for Complexity: Utilize multi-variable CERs for complex projects where multiple factors interact. While single-variable models offer simplicity, multi-variable models more accurately reflect intricate project realities, leading to more precise effort projections and schedule durations.

3. Integrate Probabilistic Modeling

Moving beyond single-point estimates by embracing probabilistic modeling significantly enhances accuracy. By quantifying cost uncertainty and risk exposure through techniques like Monte Carlo simulation, organizations gain a comprehensive understanding of possible outcome ranges. This provides more realistic confidence intervals for estimates, supporting risk-informed decision-making and ensuring that forecasts reflect the full spectrum of potential realities.

4. Leverage Expert Judgment & Iterative Refinement

Combining data-driven models with seasoned expert judgment provides a powerful synergy for accuracy. Experts can validate model outputs, interpret results within specific project contexts, and identify unique factors that might require adjustments not captured by historical data alone. 

Adopting an iterative refinement approach, starting with simpler models and gradually adding complexity, allows for continuous validation and improvement, ensuring that estimation models evolve in accuracy alongside project experience.

What Is Parametric Estimating Software and Why Is It Used?

Parametric estimating software comprises specialized mathematical models or algorithmic models designed to automate and enhance the process of generating project forecasts. These advanced tools apply parametric principles to rapidly calculate costs, schedules, and resources based on user-defined parameters and extensive historical data. They serve as powerful computational engines that replace manual, labor-intensive calculations, significantly improving the speed, consistency, and accuracy of project estimation.

When is Parametric estimating software Used and By Whom?

Parametric estimating software is primarily used in the early phases of the project lifecycle, particularly during conceptual and preliminary design stages. It becomes indispensable when:

• Information is limited: Teams need quick, defensible estimates before detailed specifications are available.
• Rapid analysis is required: Multiple scenarios or alternatives need to be evaluated swiftly.
• Statistical confidence is needed: Stakeholders demand quantifiable confidence intervals and risk exposure analysis.
• Complexity is high: Projects involve intricate relationships where manual calculations or simple analogies would be unreliable.
• Regulatory compliance is a factor: Organizations require auditable, transparent, and defensible estimates.

This software is utilized by a wide range of professionals, including:

• Project Managers: For high-level planning, strategic decision-making, and setting realistic expectations.
• Estimators: To generate accurate and verifiable forecasts efficiently.
• Cost Analysts: For detailed cost forecasting, risk quantification, and model calibration.
• Engineers: To assess design trade-offs and understand the cost implications of technical choices.
• Executives: For portfolio management, resource allocation, and go/no-go decisions.

Popular Parametric Estimating Software Solutions

The most popular parametric estimating software solutions available in the market are SEER, PRICE® Cost Analytics, COCOMO II and Deltek. SEER is an AI-powered parametric estimating software which represents one of the industry’s most comprehensive and advanced implementations of parametric estimation principles inside a software, to be used across multiple domains. It enables cost engineers, program managers, and decision-makers to turn estimation theory into execution-ready forecasts – with transparency, speed, and regulatory alignment.

SEER’s Use of Historical Data and Industry Benchmarks in Parametric Estimation

SEER Platform helps organizations compute the parametric estimates. It uses historical and market data, incorporating extensive datasets and industry benchmarks that form the foundation for their parametric models. These databases provide:

• Normalized cost data across thousands of projects.
• Industry-specific metrics and benchmarks.
• Typical parameter ranges for different project types.
• Statistical relationships validated across multiple organizations.

This data foundation allows organizations to leverage broader industry experience, calibrating models to their specific performance characteristics and ensuring historical data accuracy.

Comprehensive Parametric Models:

SEER modules contain built-in mathematical models tailored to diverse project types:

• For software development, SEER uses parameters like: functional size measures (e.g., function points, lines of code), architecture complexity ratings, implementation language characteristics, team capability factors, and development environment constraints.
• For hardware engineering, SEER incorporates: component counts and types, manufacturing complexity factors, testing requirements, integration complexity, and technology maturity levels.
• For manufacturing cost prediction, SEER models: material requirements, process complexity, production volumes, quality specifications, and tooling requirements.

Uncertainty Quantification and Risk Analysis:

A key strength of the SEER implementation is its thorough approach to uncertainty modeling. This capability enables risk quantification and risk analysis through:

• Input parameter ranges with confidence levels.
• Monte Carlo simulation with thousands of trials.
• Correlation modeling between uncertain variables.
• S-curve generation showing outcome probability distributions.
• Risk factor identification and sensitivity analysis.

This comprehensive uncertainty modeling provides decision-makers clear visibility into confidence levels and risk exposure.

Scenario Modeling for Trade Studies:

The SEER platform enables rapid scenario comparison to support design optimization and trade studies. Its capabilities include:

• Side-by-side comparison of alternative approaches.
• Parameter sensitivity analysis to identify critical variables.
• What-if capability to evaluate design changes.
• Schedule-cost-quality trade-off visualization.

This multidimensional analysis often reveals counterintuitive insights. For instance, an option with higher initial costs may actually represent the lowest total program risk when all factors are considered. Such a holistic evaluation helps teams avoid the common pitfall of choosing approaches based solely on upfront costs without considering lifecycle implications.

Scenario Analysis for Informed Decision-Making:

Leading aerospace organizations apply comprehensive cost modeling techniques using SEER to conduct scenario analysis. By modeling multiple options with consistent parameters, teams can assess direct production costs, schedule implications, quality factors, and overall program risk, thereby facilitating more informed decision-making.

Why is Parametric Estimating Especially Important for Large and Complex Projects? 

Parametric estimating is important for large and complex projects because parametric estimating uses historical data and measurable variables to produce reliable cost and schedule forecasts. Parametric estimating processes extensive historical datasets and manages multiple interrelated factors simultaneously, providing a structured and scalable framework for project planning. 

In large scale projects, parametric estimation provides essential insights at every stage: 

1. Go/No-Go Decisions: Parametric estimation compares proposed budgets to historical data, revealing gaps between initial forecasts and realistic outcomes, and enables early informed adjustments to scope and resources.
2. Design optimization: Parametric estimation evaluates alternative solutions across cost, quality, reliability, and schedule, supporting evidence-based design decisions. 
3. Project Control and Forecasting: Parametric estimation establishes performance benchmarks and highlights deviations during project execution, allowing for prompt corrective action. 
4. Post-Project Learning: Parametric estimation facilitates continuous improvement by comparing actual results to predictions and refining future models.